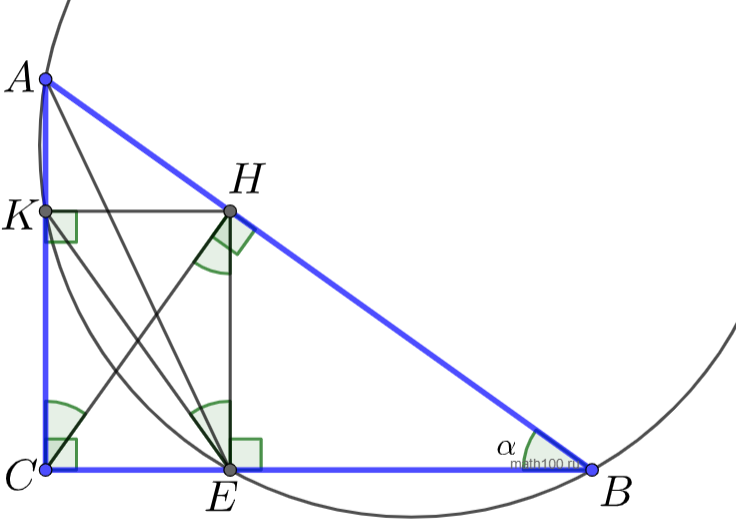
а) Пусть точка E лежит на катете BC, а точка K – на катете AC. Четырёхугольник CKHE является прямоугольником. Пусть \(\angle ABC = \alpha ,\) тогда:
\(\angle BCH = {90^ \circ } — \alpha ,\,\,\,\,\,\angle KCH = \angle CHE = \angle KEH = \alpha .\)
Следовательно, \(\angle BEK = {90^ \circ } + \alpha ,\) а \(\angle KAB = {90^ \circ } — \alpha .\)
Значит, \(\angle BEK + \angle KAB = {180^ \circ }.\) Сумма двух противоположенных углов в четырехугольнике равна \({180^ \circ }\), следовательно, четырехугольник ABEK вписан в окружность. Что и требовалось доказать.
б) Радиус окружности, проходящей через точки A, B и E равен: \(R = \dfrac{{AB}}{{2\sin \angle BEA}}.\) Так как углы BEA и AEC смежные, то \(\sin \angle BEA = \sin \angle AEC.\) Следовательно, \(R = \dfrac{{AB}}{{2\sin \angle AEC}}.\) Из равенства углов ABC и CHE следует подобие прямоугольных треугольников ABC и CHE. Из подобия этих треугольников:
\(\dfrac{{CE}}{{CH}} = \dfrac{{AC}}{{AB}}\,\,\,\,\, \Leftrightarrow \,\,\,\,\,CE = \dfrac{{CH \cdot AC}}{{AB}}.\)
Тогда:
\(AE = \sqrt {C{E^2} + A{C^2}} \, = \sqrt {\dfrac{{C{H^2} \cdot A{C^2}}}{{A{B^2}}} + A{C^2}} = AC \cdot \sqrt {\dfrac{{C{H^2} + A{B^2}}}{{A{B^2}}}} = \,\,\dfrac{{AC}}{{AB}} \cdot \sqrt {C{H^2} + A{B^2}} .\)
По определению синуса из треугольника ACE: \(\sin \angle AEC = \dfrac{{AC}}{{AE}} = \dfrac{{AB}}{{\sqrt {C{H^2}\,\, + \,\,A{B^2}} }}.\) Из этого следует, что радиус равен:
\(R = \dfrac{{AB}}{{2\sin \angle AEC}} = \,\,\dfrac{1}{2} \cdot \sqrt {C{H^2} + A{B^2}} = \dfrac{1}{2}\sqrt {{5^2} + {{12}^2}} = \dfrac{{13}}{2}.\)
Ответ: \(\dfrac{{13}}{2}.\)